Search Algorithm
Search algorithm design for the Quadrotor SAR project.
Table of Contents
Search Algorithm Design
We considered several different search algorithms for our project, including cartesian search grids, decentralized waypoint searches, and spiral search paths, considering the fact that our quadrotors could search a large area unhindered by terrain.
What we decided to implement in our system, despite the fact that it may be less efficient, is a ‘sinusoidal’ path in polar coordinates, which allowed us to increase the number of quadrotors arbitrarily and to designate a general trajectory while maximizing search coverage of an area.
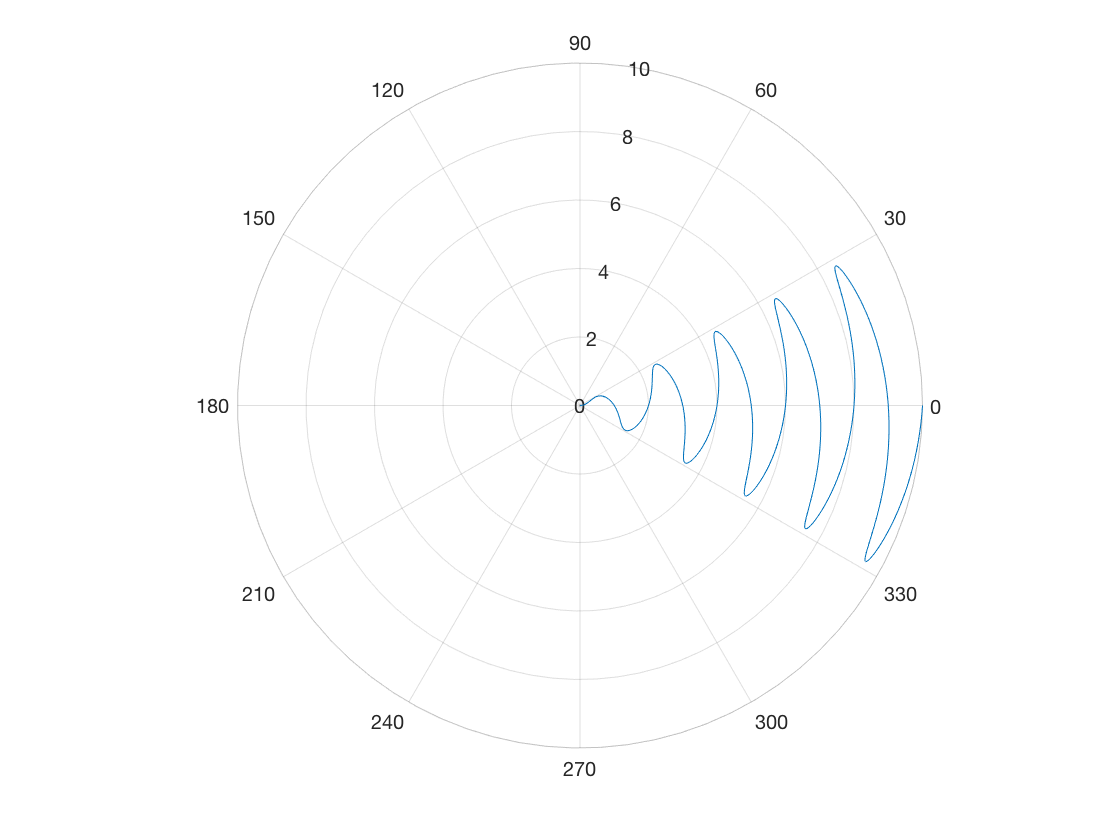
Polar Sine Pattern
We decided that using polar coordinates was desirable, mainly due to the fact that the quadrotors would not always be in range to communicate with each other or with the rescuer. We first investigated whether or not a search path such as the one below was adequate for our needs, but felt there was too much area that would be left unsearched, and that if the person was in an area that didn’t overlap with the search path, the quadrotor would not detect them, or would take a long time to find them.
Additional quadrotors could be offset by a number of degrees, increasing the coverage area, but we thought that this would require more quadrotors than might be available. We wanted the system to work with only a single quadrotor, as well as a swarm. Also, we wanted to be able to point the quadrotor in one direction, and a polar sine pattern is not conducive to this behavior.
If we increased the coverage of a single quadrotor, it meant that a person who was offset from the original angle by 90 degrees would take the longest to find, and in search and rescue, time is a critical factor.
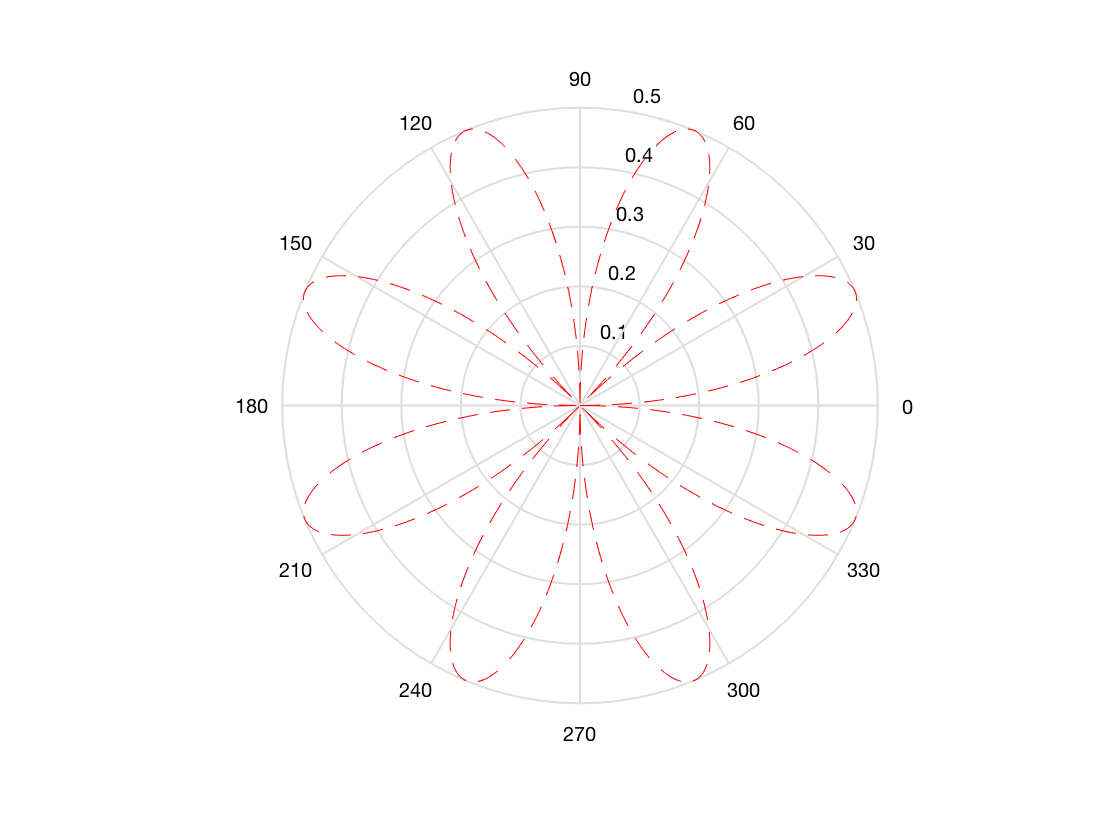
theta = 0:0.01:2*pi;
rho = sin(2*theta).*cos(2*theta);
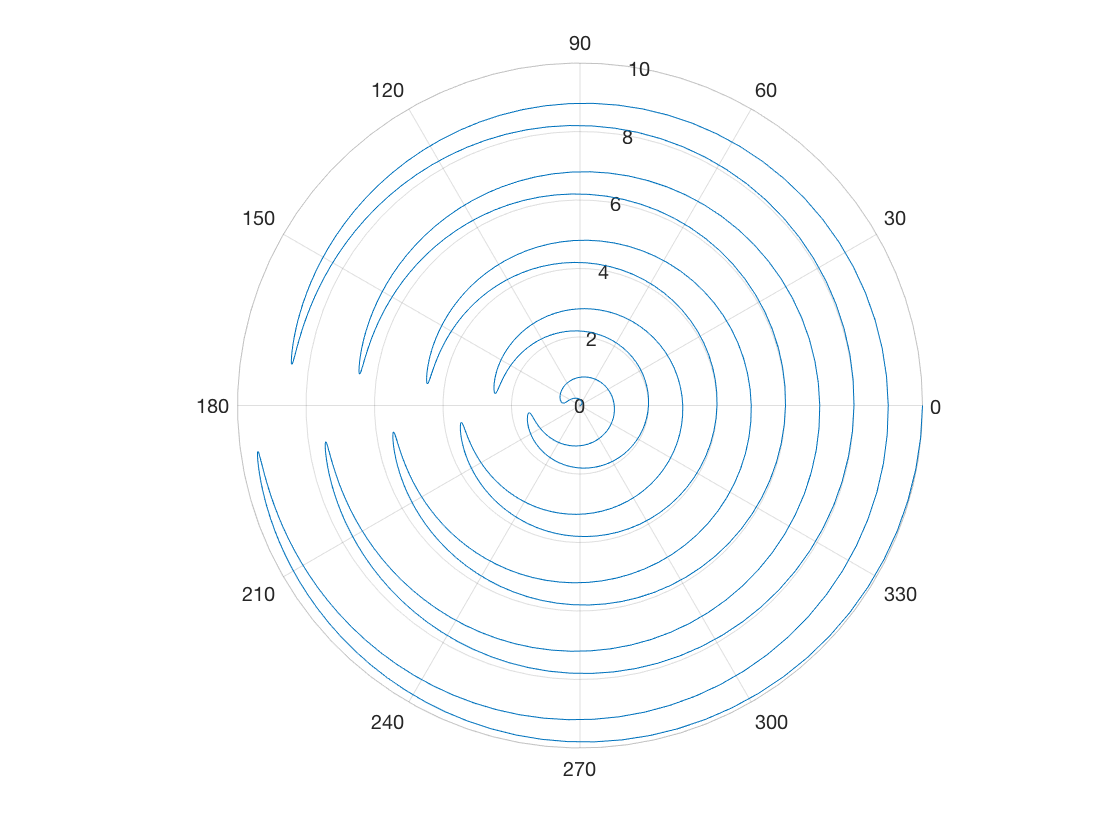
Spiral Pattern
By setting the radial coordinate equal to the angle, we could create a spiral pattern for the search and rescue quadrotors, varying the coefficients for each successive quadrotor to ensure they don’t overlap (something like 0.4, 0.7, 1.7, 2.7, etc.), but we would sacrifice a lot of time flying over areas that are close or very near to areas that other quadrotors have already searched, and a person in need of rescue would see potentially several quadrotors fly nearby, but not necessarily in the path necessary to detect them.
Additionally, a single quadrotor with a dense spiral would take a lot of time to find their target, which meant an increase in time it would take to find a person. We wanted to maintain the ‘sweep’ pattern that a lot of search and rescue parties use, but not make the quadrotor focus solely on one area. Similar to the polar sine pattern, we cannot point the quadrotor in a direction with this pattern.
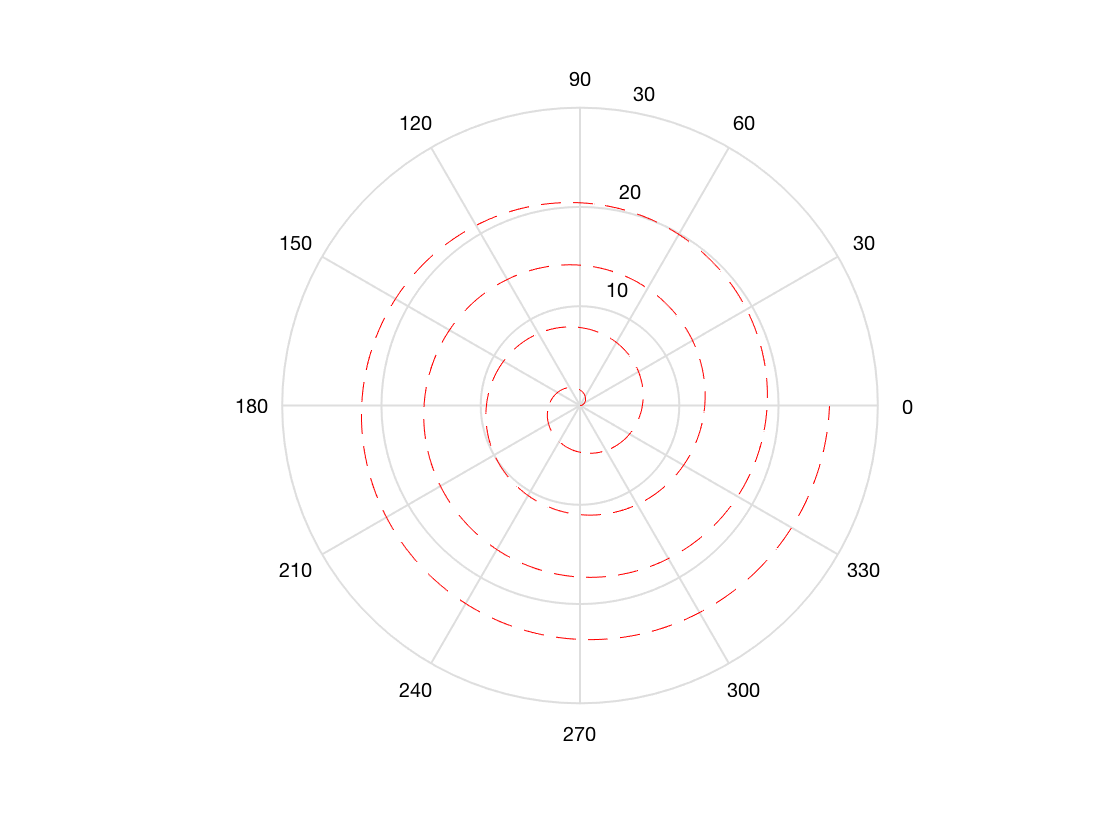
theta = 0:0.01:8*pi;
rho = theta;
Proposed Solution
What we decided in the end, which was in our opinion the fastest method with the most ground coverage, was an expanding wave in polar coordinates that emanated from the origin, bounded by two angles determined at the start by the number of quadrotors in the swarm. This means that as the number of quadrotors increases, we achieve better and faster coverage of an area, with little overlap, and are able to arbitrarily increase the number of search quadrotors.
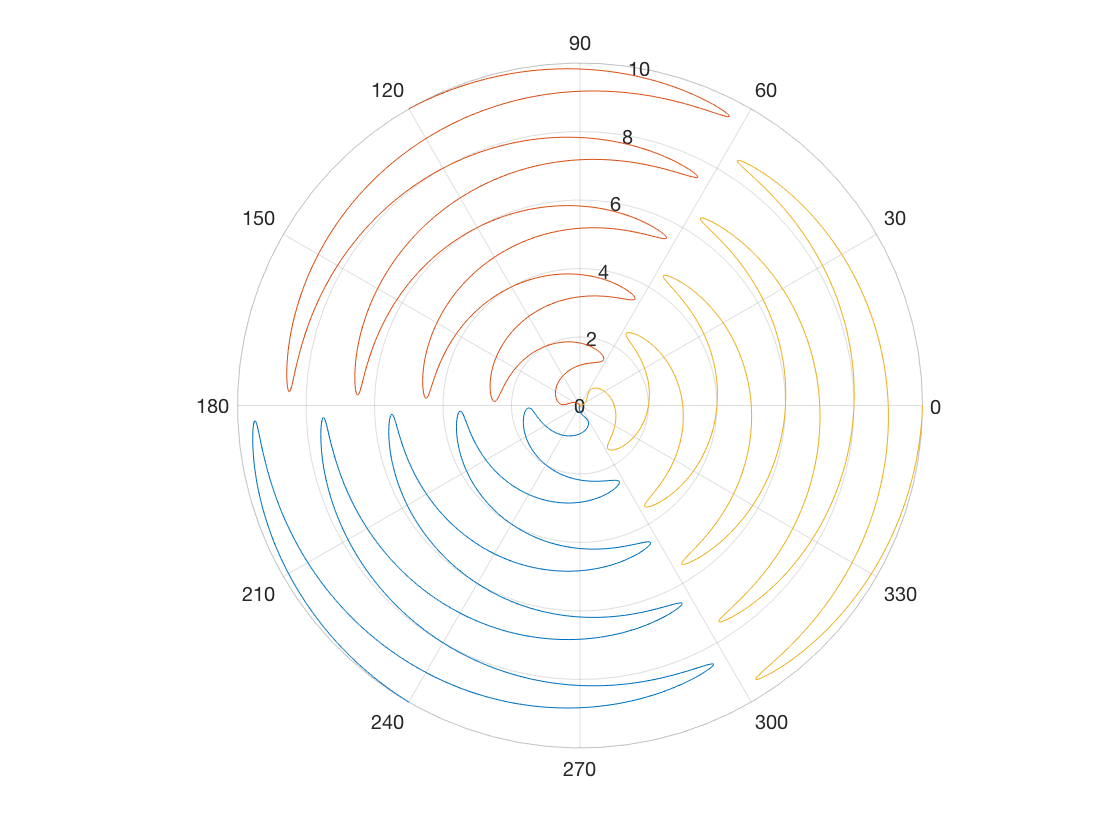
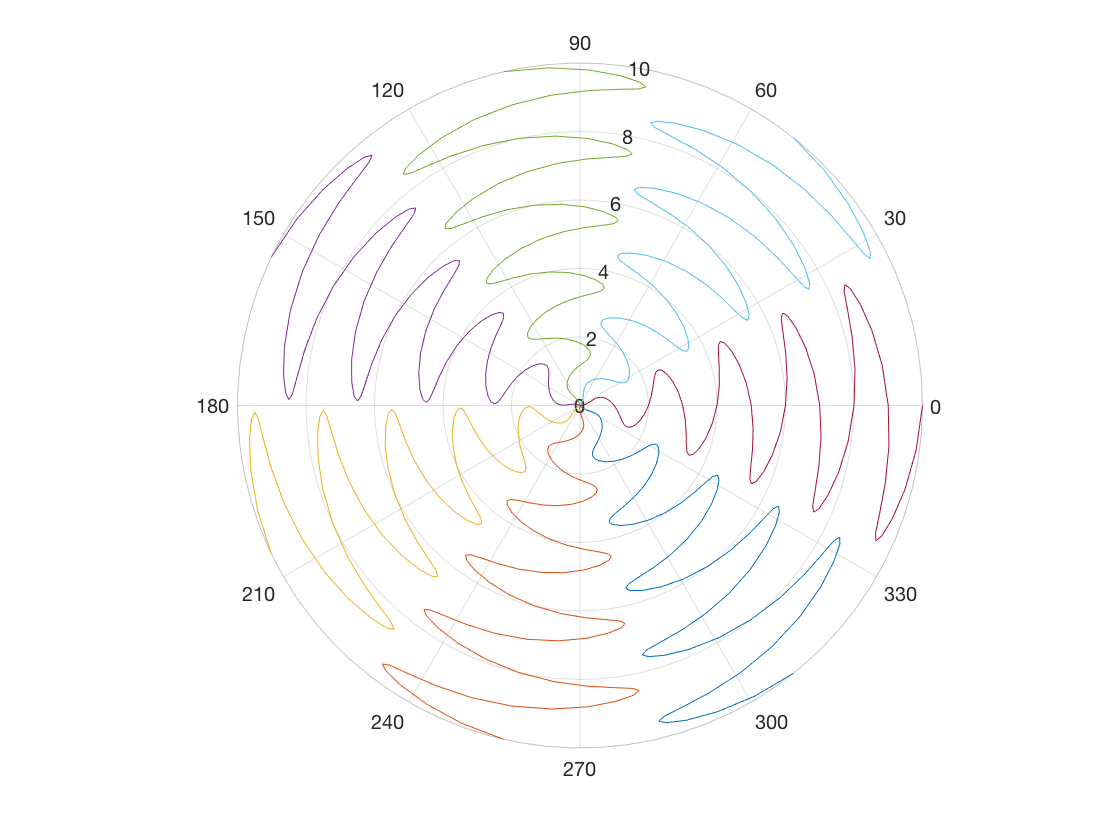
numQuadrotors = 7;
a = 3*(1/numQuadrotors);
b = 180;
b_rad = deg2rad(b);
figure
% polarplot(rho, theta)
for i = 1:numQuadrotors
c = i*(360/numQuadrotors);
c_rad = deg2rad(c);
rho = 0:0.1:10;
theta = a*sin(b_rad*rho)-c_rad;
polarplot(theta,rho)
hold on
end
hold off
We can see from the code that we have three parameters which we can alter as part of the equation governing the search parameters. We can vary a to determine the ‘amplitude’ of the sine wave, increasing the search area and angle that a single quadrotor will be able to search, we can vary the angular frequency, b, in order to increase coverage of the wedge that a single quadrotor will search, and we can vary c to change the angle the sine wave will follow.
If we hold c to be within a certain number of values, we can direct the search along a particular path, such as within a cone, rather than a circular area around the origin.
When we increase the number of quadrotors, we need to change the a constant to a value that is able to give us a wide enough search area that has no overlap.
When we have only a single quadrotor, we can sweep an entire area or just a subset of it by varying the same parameters.
Search Algorithm In Action
See the video below, which is also on our home page, to see what the search algorithm looks like in a Gazebo simulation.